- t検定とはなにか知りたい
- カイ二乗検定との違いを知りたい
- スプレッドシート(エクセル)でt検定を行いたい
統計学的検定で有名なカイ二乗検定とt検定。今回は、t検定をスプレッドシートで行う方法についてまとめていきます。
カイ二乗検定は、クロス集計された表に対して検定を行う手法ですが、t検定は連続性のあるデータに対して仮説検証を行う手法です。
それでは行きましょう!
t検定とは?
2つのデータの平均値が同じとみなせるのかどうかを調べる事ができます。
例題を見たほうが理解が早いと思いますので以下の例をご覧ください。あるクラスの上体起こしの結果です。1回目と2回目の結果をまとめています。
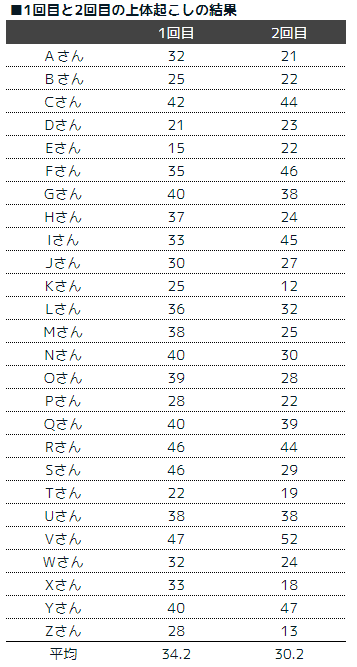
平均値を確認すると1回目が34.2、2回目が30.2と2回目の方が上体起こしの回数が減っています。偶然下がっているのか、それとも疲れなどで必然的に下がっているのかを統計学的に調べる事ができるのがt検定です。
t検定には、データに合わせて3通りの手法がある
①対応しているt検定
先ほど紹介した以下の例は、Aさんの1回目、2回目 / Bさんの1回目、2回目…となっており比較対象がペアになっています。対応しているt検定を利用して検証します。
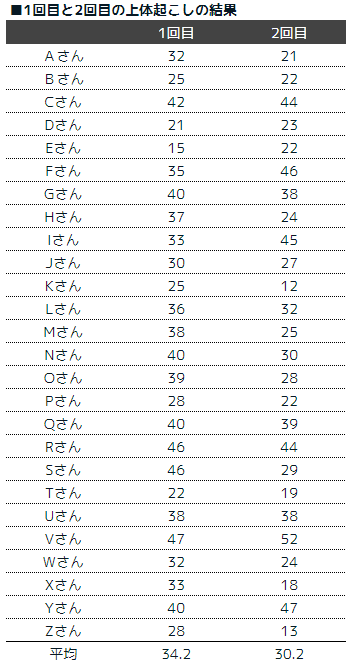
②非対応のt検定
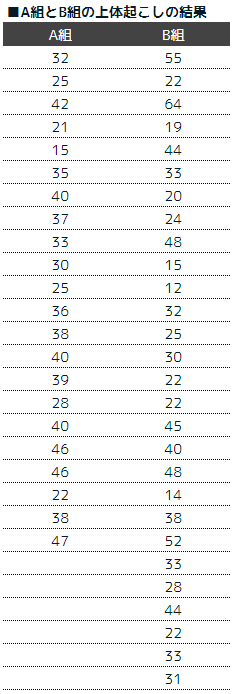
非対応のt検定では以下の様なA組とB組の上体起こしの結果を検証する場合です。A組とB組では、クラスの人数が異なり比較対象がペアになっていないケースです。
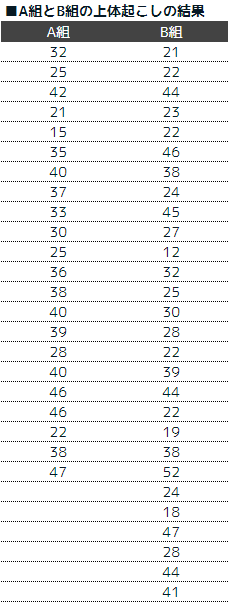
非対応のt検定では、さらにF検定というものを行います。F検定の結果、分散が同じ場合と分散が異なる場合にt検定手法が異なります。
以上のように3通りの手法が存在する事を踏まえながらそれぞれスプレッドシートでT検定を実施していきましょう。
スプレッドシートで利用する関数
t検定
= TTEST( “データ範囲1”, “データ範囲2”, “1:片側/2:両側”, “1:対応あり/2:対応なし/3:対応なし(welch)” )
F検定
= FTEST( “データ範囲1”, “データ範囲2” )
対応しているt検定をスプレッドシートで検証する
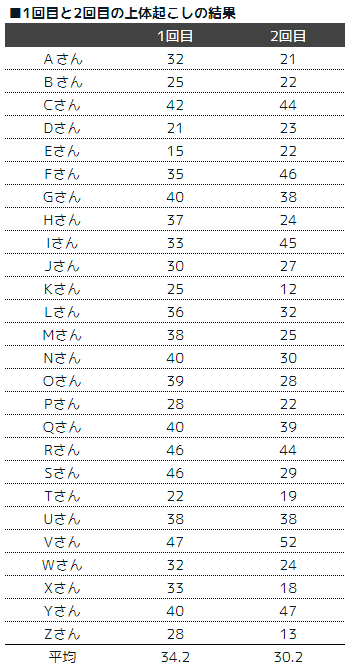
STEP1:検証手法を決める
表を見るとペアになっている事がわかります。つまり、対応するt検定を行っていきます。
STEP2:t検定を行う
=TTEST(データ範囲1、データ範囲2、片側、対応あり)で検証していきます。
つまり、 TTEST(データ範囲1、データ範囲2、1、1) となります。
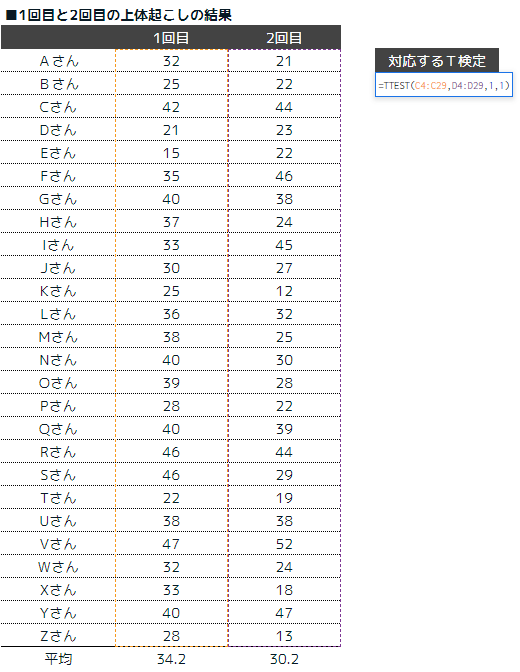
P値は、0.010602となり、有意水準0.05とした場合、有意差ありと判断できます。1回目より2回目の方が小さくなることは偶然ではないと判断できます。
非対応のt検定(分散が同じ)をスプレッドシートで検証する
STEP1:検証手法を決める
下の表を見るとペアになっていない事がわかります。つまり、非対応のt検定を行っていきます。
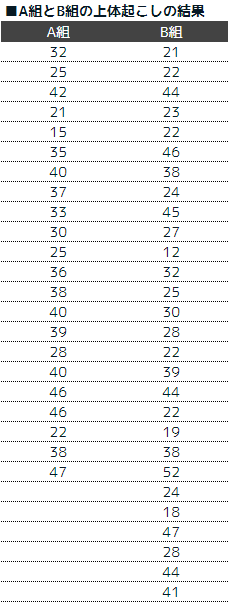
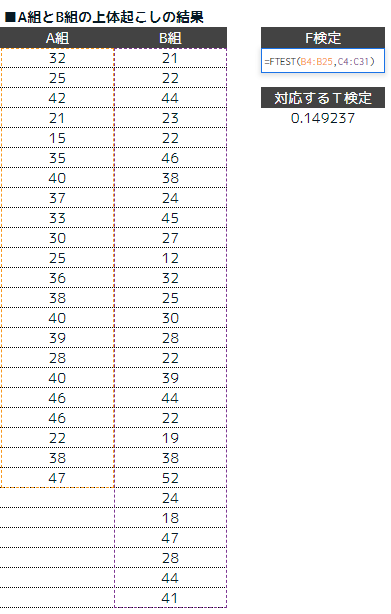
STEP2:F検定を行う
F値が0.05よりも大きければ「2つのデータの分散は同程度」と言えます。
つまり、F検定の結果は、0.290569で0.05より大きい為、非対応のt検定/分散が同じで検証していきます。
STEP3:t検定を行う
=TTEST(データ範囲1、データ範囲2、片側、対応なし)で検証していきます。
つまり、 =TTEST(データ範囲1、データ範囲2、1、2) となります。
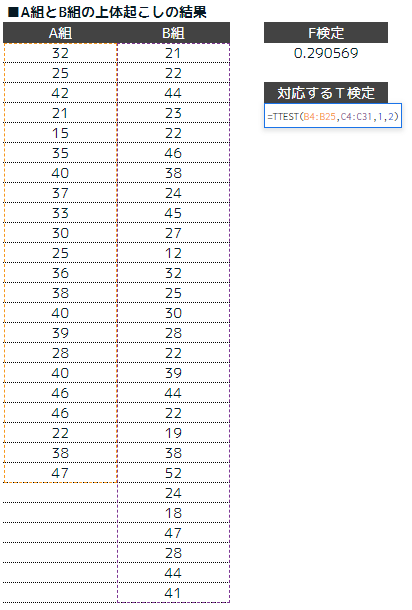
検証の結果は、0.149237であり、0.05より大きい為、有意差が確認できないと言えます。つまり、A組とB組で差はないと言えます。
非対応のt検定(分散が異なる)をスプレッドシートで検証する
STEP1:検証手法を決める
下の表を見るとペアになっていない事がわかります。つまり、非対応のt検定を行っていきます。
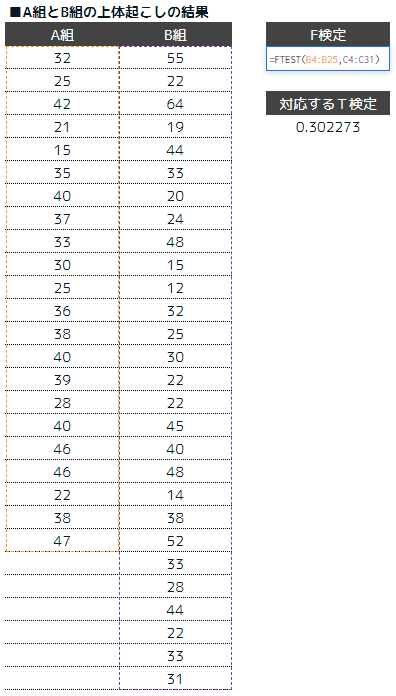
STEP2:F検定を行う
F値が0.05よりも大きければ「2つのデータの分散は同程度」と言えます。
つまり、F検定の結果は、0.045001で0.05より小さい為、非対応のt検定/分散が異なると言えます。
STEP3:t検定を行う
=TTEST(データ範囲1、データ範囲2、片側、対応なし(welch))で検証していきます。
つまり、 =TTEST(データ範囲1、データ範囲2、1、3) となります。
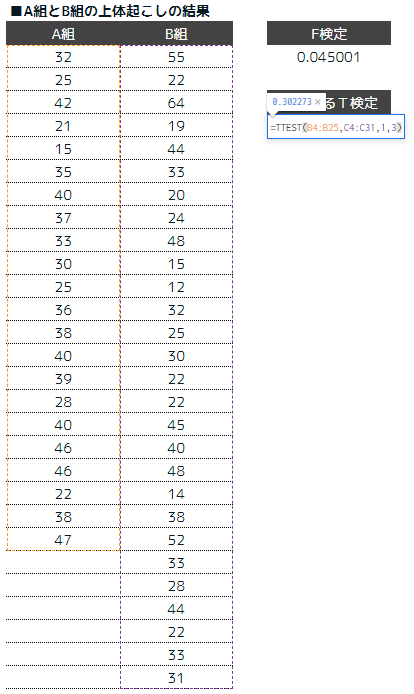
検証の結果は、0.302273であり、有意差が確認できないと言えます。つまり、A組とB組で差はないと言えます。
関連記事>>>その分析結果は偶然ではありませんか?カイ二乗検定(独立性の検定)で確かめる|CHITEST関数
